Il principio audiologico sul quale si basano gli AA analogici e quelli digitali è il medesimo cioè prelevare il segnale sonoro presente all’ingresso del microfono ed elaborarlo in base alle caratteristiche audiologiche del paziente. Dal punto di vista tecnico la differenza è notevole. La tecnologia analogica elabora un segnale elettrico la cui variazione nel tempo è continua. Quella digitale invece prevede l’elaborazione di un segnale numerico la cui variazione nel tempo avviene in modo discreto cioè non continuo. L’animazione mostra lo schema a blocchi e il principio di funzionamento di un AA digitale. Il nome digitale deriva da “Binary digits” o “bits” che significa appunto numeri binari. Un numero bianario è rappresentato da una cifra binaria cioè da uno dei due simboli che costituiscono il sistema numerico binario ovvero 0 (zero) e 1 (uno). Il sistema binario è quindi un sistema numerico che utilizza 2 simboli anziché 10 come avviene nel sistema decimale tradizionale. La matematica binaria si serve dei numeri binari per compiere qualsiasi tipo di operazione. Il byte da non confondere con il bit è la successione di 8 bit cioè otto cifre binarie combinate tra loro secondo una specifica sequenza. Nei computer un byte rappresenta il numero minimo di bit necessario a rappresentare un qualsiasi carattere alfanumerico. Un AA digitale affinché possa elaborare un segnale analogico deve trasformarlo nella forma digitale. Questo processo è realizzato mediante un dispositivo elettronico denominato convertitore analogico-digitale (A/D). Quindi all’uscita del convertitore è rilevabile un segnale digitalizzato, costituito cioè da sequenze di bit. Negli AA digitali il segnale digitalizzato è formato da una sequenza di stringhe numeriche binarie a 16 bit. Un CD player per riprodurre il suono usa lo stesso riferimento numerico a 16 bit.
Sistemi di conversione A/D.
Esistono vari sistemi di conversione del segnale da analogico a digitale. Quelli impiegati negli AA sono il PCM acronimo di (Pulse Code Modulation), Modulazione ad Impulsi in Codice e il PDM (Pulse Density Modulation) ovvero Modulazione a Densità di Impulsi. La conversione avviene grazie a due processi che si compiono contemporaneamente: il campionamento e la quantizzazione. Il campionamento “discretizza” i valori temporali e la quantizzazione quelli di ampiezza. Tuttavia, con il termine campionamento si è soliti indicare l’intero processo di conversione.
Frequenza di campionamento (teorema di Niquist)
La frequenza di campionamento (Sampling Rate) è misurata in kilohertz (kHz, migliala di volte per secondo). Essa stabilisce con quale intervallo di tempo il segnale analogico viene convertito in forma digitale. Quindi il segnale analogico è letto ad intervalli di tempo fissi dipendenti dalla frequenza di campionamento. Maggiore è la frequenza di campionamento più brevi sono gli intervalli di tempo in cui il segnale è campionato, più accurata risulta la rappresentazione digitale del segnale analogico. Supponiamo di scegliere un certo numero di campioni dalla sinusoide rappresentata in figura.
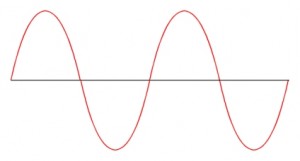
Se il numero di campioni letti è ad esempio 24 avremo una rappresentazione dell’onda simile a quella mostrata.
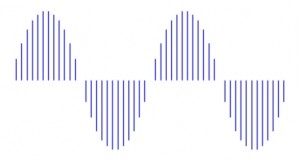
Dal punto di vista grafico la sinusoide è molto riconoscibile, cioè il numero dei campioni è tale da permettere una ricostruzione abbastanza fedele dell’onda originale. Supponiamo di dimezzare la frequenza di campionamento, ovvero di raddoppiare il tempo tra una misurazione e l’altra. In questo caso avremo la metà dei campioni letti cioè 12.

E’ evidente una certa perdita di informazioni, tuttavia la sinusoide originaria è ancora abbastanza leggibile. Se dimezziamo ancora la frequenza di campionamento, l’onda diviene sempre più irriconoscibile.

Pertanto in base al procedimento descritto è possibile affermare che la perdita di informazioni aumenta al diminuire della frequenza di campionamento. Essa quindi non può scendere oltre un certo limite. Il Teorema di Nyquist fissa appunto il limite oltre il quale si verifica una perdita totale di informazione. Esso afferma che:
ogni segnale a banda limitata può essere campionato e perfettamente ricostruito a patto che la frequenza di campionamento sia almeno il doppio della frequenza massima contenuta nella banda del segnale. In altre parole la frequenza più alta riproducibile da un sistema digitale è pari o minore alla metà della frequenza di campionamento.
Quindi il teorema di Nyquist è importante al fine di stabilire quale sia la massima frequenza riproducibile del segnale sonoro. La frequenza massima riproducibile è anche conosciuta come limite di Nyquist. Poiché l’organo uditivo umano è in grado di percepire frequenze comprese tra 20 e 20 kHz, la frequenza di campionamento deve essere almeno di 40 kHz cioè il doppio della massima frequenza udibile dal nostro sistema uditivo. La frequenza di campionamento per un CD convenzionale è fissata a 44,1 kHz. Per altri scopi sono utilizzate anche frequenze di campionamento più alte (48-96 kHz), o più basse (15-30 kHz). La maggior parte degli AA impiega una frequenza di campionamento di 32 kHz. Gli AA possono quindi riprodurre un segnale audio ad alta fedeltà con una larghezza di banda massima di 16 KHz. Tutte le frequenze sopra questo limite (frequenza di Nyquist) vengono tagliate mediante un filtro passa-basso al fine di prevenire l’effetto aliasing.
Aliasing
Il fenomeno dell’aliasing si verifica quando il rapporto tra la frequenza di campionamento e la frequenza massima del segnale analogico in ingresso è inferiore a 2. In questo caso si ha una errata interpretazione dei campioni letti che genera la riproduzione di un segnale sinusoidale anomalo la cui frequenza vale:
Faliasing = Fcampionamento – F
Dove F è frequenza del segnale analogico di ingresso eccedente il limite di Nyquist. Ad esempio un segnale sinusoidale con una frequenza 3,2 kHz campionato alla frequenza di 4 kHz è interpretato dopo la conversione come un segnale la cui frequenza vale 0,8 kHz.
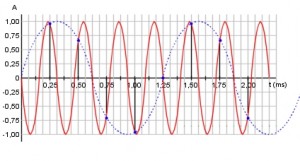
La curva rossa rappresenta un segnale sinusoidale con frequenza di 3,2 kHz. Il campionamento avviene ogni 0,25 ms corrispondenti ad una frequenza di campionamento di 4 kHz.. La linea blu tratteggiata mostra il segnale di aliasing a 0,8 kHz generato dagli errori di campionamento.
Quindi nelle forme d’onda complesse, il fenomeno dell’aliasing introduce tante componenti sinusoidali estranee allo spettro quante sono le frequenze che superano il limite di Nyquist. Poiché il filtro passa basso detto anche antialiasing è il primo dispositivo che il segnale incontra durante il processo di conversione, esso deve rispondere a requisiti di elevata qualità al fine di evitare possibili degradazioni del segnale stesso.
Quantizzazione.
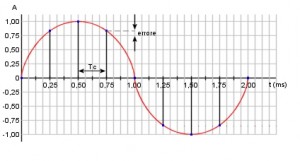
Durante il processo di conversione digitale la lettura del segnale analogico avviene secondo due coordinate. Quella del tempo, il cui dominio è affidato alla frequenza di campionamento. E quella dell’ampiezza il cui dominio è affidato alla profondità in bit o risoluzione. Il segnale analogico è campionato in base ai valori assunti dai punti di intersezione delle due coordinate. In questo modo si origina una griglia in cui il numero dei punti di intersezione dipende dalla frequenza di campionamento e dalla profondità in bit. La quantizzazione consiste nell’assegnare ad ogni lettura d’ampiezza un valore corrispondente a quello del punto più vicino disponibile sulla griglia. Questa operazione presuppone un arrotondamento per eccesso o per difetto del valore d’ampiezza effettivo a quello relativo prossimo disponibile. La figura mostra infatti che il valore 0,85 (valore effettivo) è approssimato per difetto a 0.75 (valore relativo) prossimo al punto di incrocio della griglia.
Ciò determina un errore che aumenta al diminuire della risoluzione. Pertanto più alta è la profondità in bit, maggiore è il numero dei livelli di quantizzazione, minore è l’errore che si genera. Questo errore prende il nome di errore di quantizzazione il suo effetto produce un segnale indesiderato detto rumore di quantizzazione. Inoltre il valore d’ampiezza relativo è mantenuto costante (holding completo) per un tempo pari al periodo di campionamento Tc, in questo modo si introduce una ulteriore deformazione del segnale campionato (funzione a gradini).
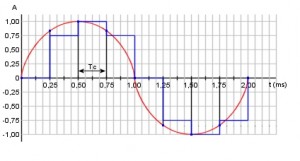
Conversione numerica di un segnale analagioco con holdin completo (funzione a gradini). La curva blu rappresenta la forma d’onda del segnale sinusoidale dopo il campionamento effettuato ad una frequenza di 4 kHz con 9 livelli di quantizzazione.
I dispositivi di conversione PCM attribuiscono ad ogni livello di quantizzazione una stringa binaria costituita da un numero di cifre binarie dipendente dalla capacità di elaborazione del processore. Ad esempio un convertitore A/D a 4 bit, ha una capacità di elaborazione a 4 cifre binarie da 0000 a 1111 in questo caso la combinazione dei valori possibili è 24 =16. Ricordiamo che il numero di combinazioni che può assumere una stringa di bit costituita da n cifre binarie è dato da 2n. Pertanto l’ampiezza del segnale in un preciso istante assume uno dei 16 valori binari disponibili. La codifica a 4 bit possiede una bassa risoluzione poiché genera solo 16 livelli di quantizzazione. Con 8 bit si possono codificare 286 = 256 livelli di quantizzazione. Con una codifica a 16 bit, attualmente impiegata negli AA si possono codificare 216 = 65.536 livelli di quantizzazione. In questo caso, l’intera gamma dinamica del segnale di ingresso è espressa su 65.536 valori. L’aumento esponenziale delle combinazioni possibili determina per ogni incremento di un solo bit nella codifica della stringa binaria, un raddoppio del numero di livelli rappresentabili. L’impiego di un maggior numero di livelli di quantizzazione permette di aumentare il range dinamico e allo stesso tempo migliorare la risoluzione del segnale audio. La figura mostra che passando da una codifica di 8 a 16 bit a parità di frequenza di campionamento la risoluzione della sinusoide aumenta.
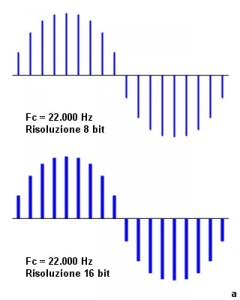
Frequenza di campionamento 22.000 Hz.
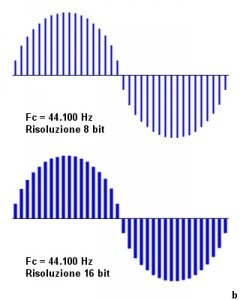
Frequenza di campionamento 44.100 Hz.
Il sistema di conversione PCM con codifica a 16 bit garantisce l’elaborazione di ampie escursioni del segnale di ingresso mantenendo una elevata gamma dinamica e un basso errore di quantizzazione. La prima colonna della tabella successiva mostra il range dinamico RD in funzione del numero di bit di codifica. La formula da cui si ricava il valore espresso in dB del range dinamico è la seguente:
![]()
La seconda colonna mostra invece il rapporto segnale rumore S/N sempre in funzione del numero di bit di codifica per un segnale che occupa l’intero range del quantizzatore. La formula che esprime il valore in dB del rapporto segnale rumore è la seguente:
S/N = 1,76 + 6,02·n
Dalla formula si deduce che per ogni bit aggiunto alla codifica il rapporto S/N cresce di circa 6 dB. Con una codifica a 16 bit il range dinamico è di 96,32 dB e il rapporto S/N è di 98,08 dB più intenso rispetto al rumore di quantizzazione.
Gamma dinamica e rapporto S/N in funzione del numero di bit del convertitore. |
||
| Numero di bit di codifica | RD (dB SPL) | S/R (dB SPL) |
| 8 | 48,16 | 49,92 |
| 9 | 54,18 | 55,94 |
| 10 | 60,20 | 61,96 |
| 11 | 66,22 | 67,98 |
| 12 | 72,24 | 74,00 |
| 13 | 78,26 | 80,02 |
| 14 | 84,28 | 86,04 |
| 15 | 90,30 | 92,06 |
| 16 | 96,32 | 98,08 |
Un CD player per riprodurre il suono usa una codifica a 16 bit. Tuttavia è improprio attribuire il termine di qualità CD agli AA. La qualità CD misurata in camera anecoica cioè in condizioni ideali assicura un rapporto S/N che si avvicina a quello teorico di 98,08 dB SPL. Purtroppo negli AA il rapporto S/N è molto inferiore a causa del rumore di fondo di circa 20 dB introdotto dal microfono.




Leave A Comment
You must be logged in to post a comment.